cap decoupling of triodes /2

This is part 2 (out of 4) of the lecture that I held at the 2015 European Triode Festival (ETF). It is about new insights, new graphs and new formulas that I developed during 2015 for cap decoupling of resistance-loaded triode gain stages.

note: if the terms ‘right-sized time constants’, ƒ_interest, ƒ_-3dB, hippies, or ‘Nixonian decoupling strategies’ do not sound familiar to you, then I recommend that you start off by (re)reading part one.

In this instalment we will look at B+ decoupling in isolation—

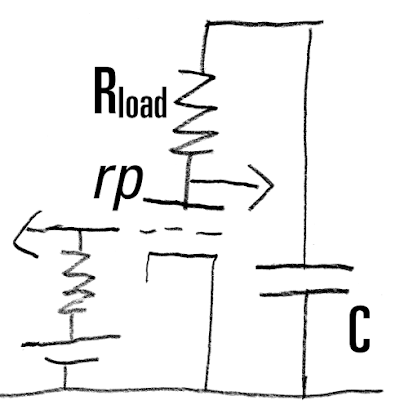
Note that the tube is fixed-biased through a battery on the grid; there is nothing in the kathode circuit that needs to be taken into account.

We see a triode with plate resistance rp, loaded by a resistor R_load, being decoupled by B+ capacitor C. The capacitor closes the AC loop for currents that need to make it from ground back to B+—currents local to this tube and the ones that flow into whatever follows this stage. One thing I had to clarify for myself earlier this year was: the cap decouples a certain resistance and forms the time constant with this resistance; is it R_load, rp, or what?

To find out, I made a frequency response plot of a 7k rp triode with a 20k R_load and a 20k triode loaded by 7k (yes, you are allowed to do that; I call it pentode mode), both decoupled by 1µF:

(x: frequency in octaves, 0=20Hz; y: decibels)

We see a clear difference in gain between the two, but they roll off at exactly the same frequency; -3dB at 5.9Hz—that of 1µF and 27kΩ. Thus I learned that the cap is decoupling the tube and the load. Now let us define an ideal capacitor:

C_ideal = 1 / [2π(rp + R_load)ƒ_-3dB]

It is the cap value that decouples the tube and load exactly at the ƒ_-3dB that you arrived at in the first instalment. I can already divulge that in this whole series it will never get better/lower than this; this cap value is indeed the ideal one. I will now go through some example values of C_ideal—I rolled the dice for a ƒ_-3dB and… all of them are @3Hz.

6sn7, R_load = 24k, C_ideal = 1.7µF. You see, it does not take much to decouple this general-purpose driver tube.

26, R_load = 24k, C_ideal = 1.7µF. Different tube, same impedances, same cap value.

ecc83, R_load = 100k, C_ideal = 0.33µF. Everybody’s friend; it takes only a fraction of a microFarad to decouple it.

ecc88, R_load = 10k, C_ideal = 4.2µF. In comparison, for this popular tube the cap is a factor twelve larger.

ec8020, R_load = 2k2, C_ideal = 17µF. Now for something real hot and racy; still does not require 47µ, does it?

el34(triode), R_load = 2k2, C_ideal = 17µF. I wanted to round off this overview with a stout (power) driver tube—turns out it has the same 900Ω plate resistance as an ec8020; same load, same ideal cap value.

paradise lost

Those ideal cap values look really appealing to me (you know my hidden agenda, right?). But now we will find out why I called them ideal; usually we can royally forget about using caps that low in value. This is because the B+ cap performs a second job in collaboration with another resistor:

The B+ cap filters the B+ together with R_filter. There is a whole list of reasons for this—

1. filter some more hum and noise, especially for stages early in the amplifying chain;
2. keep the AC currents local to this stage; R_filter stops them from going elsewhere;
3. if you got stages that are working in phase on the same B+, then you can get motor-boating because of positive feedback at low frequencies via the B+ line from a later stage (more mayhem) to an earlier one (more sensitive); this filter suppresses that;
4. if you can get positive feedback between stages that are in phase, then I expect negative feedback, at low frequencies, between stages that are out of phase—also suppressed.

That’s all great, but what’s a good time constant for this B+ filter? I had to admit earlier this year that I had no clue. Could I come up with a theory? Nah, better not.

census

Instead, I took an empirical approach. I went through the whole Sound Practices CD and looked at every schematic. This gave me a curated collection of historical classics and ultra-fi designs from the 80s and 90s. I used the following criteria—

1. multi-stage amp
2. with RC B+ filtering
3. and unambiguous values (what is MMF? I am not going to guess…)

I calculated the time constant of the B+ filters that qualified, and sorted them into a histogram:

I used the E6 series for the centre values of the bars. The resulting histogram shows a preference for highish values, I must say. For comparison: the 3Hz that I used above for the ideal capacitor examples has a time constant of 0.053. What I see in this histogram are trends centred on three peaks. I can name the outer two:

with the largest one in the middle being the silent majority. In left field (below 0.022) we see some really enlightened—or spaced out—design decisions

context, context, context

Now I had a spread of values, but… compared to what? Here is another design thing: designers know that one cannot take a solution that works in one context and just apply it in a different one (refusing to ‘just copy it’ creates quite a bit of strife with all the non-designers they work with). In this case I could not apply the B+ filter time constant wisdom of the SP/historical context to my own private one (my ƒ_-3dB).

I needed to compare the B+ filter time constant spread to the ƒ_-3dB of the same context and learn from that. Luckily, there is such a thing: the time constants of the coupling caps. These are straightforward to calculate and an unambiguous expression of ƒ_-3dB.

Thus I returned to the Sound Practices CD and went again through all the schematics. I used the following criteria—

1. multi-stage amp
2. with RC coupling
3. and unambiguous values

I calculated the time constant of all the RC coupling that qualified, and sorted them also into a histogram:

Note that the horizontal range is that same as for the B+ filter. The spread of values is positioned more to the left. Again I see trends centred on three peaks:

with the largest one in the middle being the silent majority. While compiling the histogram I noticed the reason for the smallest time constants (some of the 0.01, and all below that): all of these are in global feedback amps and with their low value ensure that the amp—with feedback applied—does not end up having some crazy low cut-off, like 0.5Hz (there is a lesson in there for all of us).

Also I like to bring to your attention to that lone far-right position (a blip at 2.2). It is from SP15, the R120 amp. A 2µF coupling cap, or a 1Meg grid resistor are large, but the combination is outrageous.

Now we can put the two histograms together and observe how the three peaks relate:

The hippies moved a factor five to the right, as did the silent majority. Nixon moved to the right by a factor of ten. My conclusion—

B+ filter time constants are five to ten times stiffer than that of your ƒ_-3dB.

That’s right, you can take your own ƒ_-3dB, divide it by 5–10, depending on where you are on the hippie–to–Nixon spectrum, and size your B+ filter for that value.

With hindsight it all looks quite logical (duh…): if the ƒ_-3dB dictates the lowest frequency that makes it through the output stage of the amplifier and the B+ filter has to ensure that this frequency does not make it back to the input stage, then it needs to start filtering a decade lower, or a little less.

drifting out of reach

This “five to ten times stiffer” is going to cause us trouble. Because if we want to use the ideal capacitor value, the filter resistor has to be quite large:

What is the problem with that? DC voltage drop. R_filter will not drop exactly 5 to 10 times as much as the tube and load—the tube drops more DC than the dynamic rp would make you believe. But 4 to 8 times as much? sure. This means that 80–89% of the available B+ is not available to the tube and loading resistor.

That may not be a problem if you have 1250 Volts (or more) available as B+, but in most practical cases, for the sake of headroom and linearity, you cannot drop so many volts. In most practical circuits, R_filter will be less than (rp + R_load). In these articles we will work with the value 2–10 times less. Multiplying that out with the B+ filter requirement, we get—

In most practical circuits, the B+ capacitor will be 10 to 100 times larger than C_ideal.

That is, the B+ capacitor—and thus the decoupling time constant—will be 10 to 100 times too large in a fixed-bias triode gain stage. I must say that when I came to that conclusion earlier this year, found it quite depressing.

Is there any hope? Well, like always in tube circuits there must be multiple ways to solve this, but I can offer you just one. What we need is a modest voltage drop and relatively large resistance. There is a circuit for that, the current source:

Now don’t get overenthusiastic. I know you know a schematic for a current source that has a gazillion Ohms over a wide bandwidth. But remember, this series is all about getting things right-sized. Thus if your calculations say you need 105 kiloOhm, then it is 105kΩ you’re going to build (OK, ±10%, no need to get anal). But if you do put in a gazillion Ohms, then I predict that you will end up with stage that works like a (subtle) compressor.

Here is my simple proposal for a right-sized ‘current source’; more or less an electronic resistor:

Straight off there are two practical things that I can say about this arrangement—

1. because the purpose of this exercise is to put a generous amount of volts (say, 250–350) between the kathodes of the two tubes, it is—for heater–kathode rating reasons—almost certain that they cannot be on the same heater rail (the top tube needs a raised heater rail); thus these two tubes will not be in the same glass envelope;
2. because the purpose of this exercise is that the electronic resistor works at the same plate current as the amplifying tube, but at lower plate voltage (biassed hot) and with a much higher overall impedance, it is really unlikely that the top tube will be of the same type as the bottom one.

Finding the right tube for the electronic resistor is a nice puzzle with the tube manual. You can start out with either high plate resistance (‘almost there’), or with high µ, or both. The tube needs to be ‘switched on’ at the required voltage drop and support the required plate current. Have fun…

doggy bag

Here are the take-home points of this instalment—

• It is the tube rp and load that is decoupled by the B+ capacitor.
• There is an ideal capacitor value for decoupling the B+ at your ƒ_-3dB and its value is deliciously low;
• The other job of the B+ capacitor is to filter the… B+; the time constant for this is five to ten times stiffer than that of your ƒ_-3dB.
• In most practical circuits, the B+ capacitor will be 10 to 100 times larger than C_ideal; thus in fixed-bias circuits, the decoupling time constant will then be 10–100 times higher than you intended; hello, distorted treble.
• You can achieve the ideal capacitor value if you are either blessed with a high (1250V+) B+, or when you work real hard for it (e.g. electronic resistor).

And that’s all. Next up part three, where we will move on to the kathode decoupling.